Why do we at Northern Audio love HQPlayer? It’s all about the filters! Any DAC uses filters to achieve it’s signature sound. HQPlayer allows you to sample some of the finest filters out there, IF you have the PC power for it.
Grigg Audio Solutions in Rostock, Germany has nicely summarized why the HQPlayer’s filter properties, user interface, and high quality algorithms are masterfully combined for an unrivaled audio experience. Their information is used below with permission to help get you started.
Want to learn more? Come see us for a free consultation on how to build your Ultimate Custom HQPlayer PC or Home Theater PC! Call today at 412.931.5850.
Audio PC HQPlayer Filter Properties
Table of contents
- Filter qualities
- Pre-ringing and post-ringing
- Filters for finite impulse response (FIR – linear phase) and infinite impulse response (IIR – minimum phase)
- Effects on space and transients and music genres
- Apodizing and non-apodizing
- Upsampling ratio
- Compressed music
- Table with filter properties
Although the HQPlayer can be used as an audio player in Windows, Linux and macOS, it cannot compare to Roon in terms of ease of use. However, when it comes to upsampling, the HQPlayer is worlds better than Roon. The ability to integrate the HQPlayer into Roon means that the intuitive user interface and the highest quality algorithms can be combined.
The HQPlayer offers filters which
– are apodizing and non-apodizing, – have
different effects on space , transients and timbre
, – prefer different sampling rates (CD or HiRes),
– require low or high computing power and
– even support different music genres .
The whole thing is quite confusing, which puts many people off. We’re trying to shed some light on the matter.
Filter qualities
For a CD (44.1 kHz) the audible range may only go up to a maximum of 22.05 kHz . This is based on the Nyquist-Shannon sampling theorem , which should only take half the sampling rate ( Nyquist frequency ) into account. If the sampling theorem is violated by a sampling rate that is too low, frequency components that were originally higher than half the sampling rate are interpreted as lower frequencies, since they are undersampled. This undesirable phenomenon is called the aliasing effect . These so-called mirror frequencies should be blocked out by filters, which is why these filters are often also called anti-aliasing filters .
It therefore depends on the filter quality which frequencies are allowed through in practice ( passband ), at what point the blocking effect ( cutoff ) begins and how long it takes ( transition range ) until the low-pass filter develops its full effect ( stopband ). Independent measurements have shown that the HQPlayer filters are very well constructed.

If the blocking effect is very low , this is referred to as extremely high attenuation . This is a good thing because image frequencies are effectively suppressed. High attenuation leads to fewer noise artifacts and also to better reconstruction accuracy.
Equally important is when the cutoff begins. Some filters start in the audible frequency range, which is of course not desirable. A steep filter is also beneficial, as it achieves a very narrow transition band . If we take the example of an input rate of 44.1 kHz (CD), the passband of the “poly-sinc-gauss-xl” filter goes up to 20 kHz, the transition range is extremely narrow at 250 Hz and reaches maximum attenuation at the Nyquist frequency fs/2 at 22.05 kHz. Filters of this high quality are often referred to as having a fast or sharp “rolloff” or “cutoff” . See also:
Pre-ringing and post-ringing
Pre-ringing and post-ringing are two types of artifacts that can occur in digital signal processing. Pre-ringing is the phenomenon that a signal rises or falls before an abrupt transition or before it reaches its actual value. Post-ringing is the phenomenon that a signal oscillates after an abrupt transition before it stabilizes.
Both effects can affect the quality and accuracy of a signal and can cause audible effects. Pre-ringing in particular can be very disturbing because it does not occur in nature.
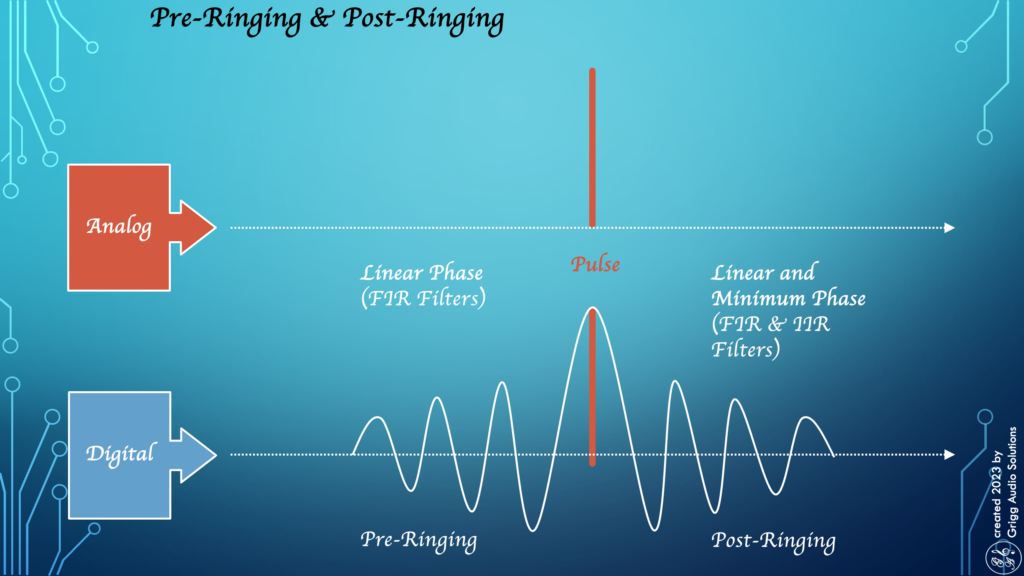
When designing a filter, it is important to keep pre- and post-echoes as low as possible. They cannot be completely avoided.
Filters for finite impulse response (FIR – linear phase) and infinite impulse response (IIR – minimum phase)
FIR and IIR filters are two types of digital filters used for signal processing. They differ mainly in their impulse response and phase characteristics.
FIR (Finite Impulse Response) filters have a finite impulse response that decays to zero after a certain time. They have a linear phase, which means that all frequencies have the same delay through the filter. They are always stable because they have no feedback loops. However, they require more coefficients and storage space than IIR filters to achieve a similar frequency response. They can also produce pre-ringing that precedes the actual impulse.
IIR (Infinite Impulse Response) filters have an infinite impulse response that decays infinitely. They have minimum phase , which means that different frequencies have different delays through the filter. They can be unstable if the feedback loops are too large, but they require fewer coefficients and storage space than FIR filters to achieve a similar frequency response. They do not have pre-ringing , but they can cause group delay distortion .
Although the lack of pre-ringing and the lower computing load speak in favor of IIR filters, the unwanted phase shifts in music playback are of course a serious problem. The linear phase of FIR filters is a strong argument for their use. Therefore, most filters in the HQPlayer are linear phase, unless otherwise stated. The following articles are suitable for further in-depth study of filter design and for listening examples of pre-ringing:
- Which EQ Filter is Best For Mixing Bass and Low-End?
- Linear and minimum phase – Troll Audio (troll-audio.com)
Effects on space and transients and music genres
The group of poly-sync-lp (linear phase) filters improve the spatiality (space). They belong to the FIR filters and work in the time domain. Recommended for classical music and for music recorded “in the real world” (concert hall). A subtype of these are the AsymFIR filters, which are particularly suitable for jazz/blues .
The group of poly-sync-mp (minimum phase) filters improve the transients . They belong to the MinPhaseFIR filters and are particularly suitable for rock/pop/electronics , as well as music recorded in the music studio. This also applies implicitly to IIR filters .
Some filters also focus on the timbre , i.e. the sound colors.
Apodizing and non-apodizing
The purpose of the apodization filter is to replace the impulse response of the original decimation filter with another one. This allows changing the time and frequency domain behavior of the original filter. A possibly more important point is to clean up the aliasing band at the highest frequencies. Depending on the ADC/mastering tools, there may be some aliasing band at the top of the frequency band. See also:
Non-apodizing filters let the (possibly faulty) production-side digital filter properties through. Non-apodizing filters are good for HiRes recordings (88.2/96kHz and above) because the Nyquist rate is very high. Apodizing filters are most important for Reedbook/CD formats (44.1/48kHz) because of the low Nyquist rate. Here is a detailed explanation from Jussi Laako:
When using oversampled PCM, it doesn’t matter if it’s an R2R or Delta Sigma converter, you’ll get exactly the same ringing behavior with both because it comes from the digital filters and not the converter technology.
Ringing is the result of band limiting, and with RedBook content or other content sampled at a very low 44.1k or 48k rate, you need strict band limiting because you need to remove all frequencies above half the sample rate, otherwise they would be down- converted to the audio band. As a result, all A/D converters producing such content oversampled using digital decimation filters to reduce the sample rate to such low rates. By the way, all current A/D converters for music recording are delta-sigma converters. This results in ringing already built into your music content from the start.
Using R2R without oversampling at these low source content rates has a number of problems:
1) You have no proper reconstruction of the original analog signal at all, so you hear a heavily distorted signal that only slightly resembles the original.
2) Your transient level and timing are wrong because the music transient never coincides exactly with the sampling moment, but happens somewhere between samples. In the worst case, it is completely lost.
3) As a result of incorrect transient timing, you suffer from jitter in your waveforms.
4) Your output will have a large spread of frame frequencies into the MHz range due to lack of reconstruction, these will have intermodulation products that reflect each other back to the audio band.
5) You will have a strong high frequency rolloff starting at 1 kHz and being strongest between 10 kHz and 20 kHz.
Anything to avoid something that is already integrated into your source code anyway.
On such a NOS R2R sine wave, the 19 kHz sine wave looks like this:
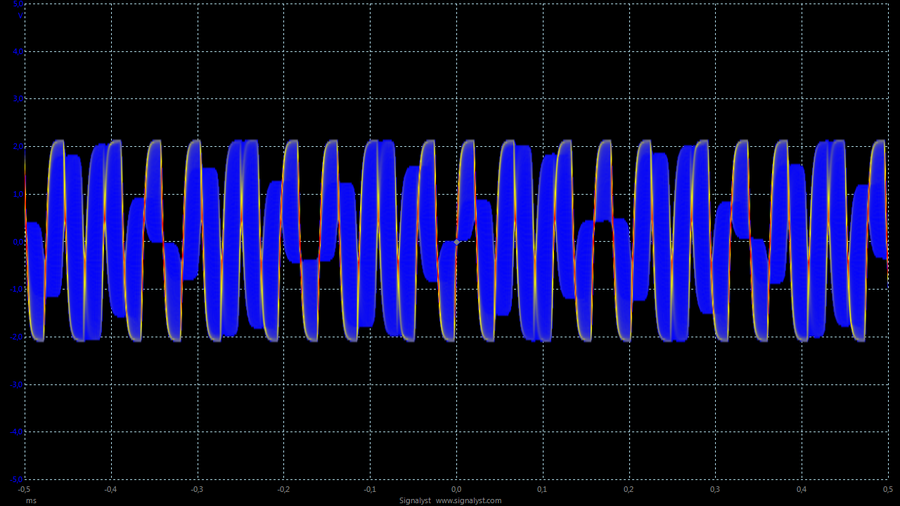
You can also see that the signal is very unstable as the waveform is filled with blue areas where the signal has occasionally touched.
Now the amount of ringing depends on the filter length (IOW, number of taps). The longer the filter (more taps), the longer it rings. So, for example, Chord’s 1 million tap linear phase filter at a rate of 705.6k means it has almost a second of pre-ringing and the same amount of post-ringing (about 500,000 samples on either side; 705.6 / 500 = 0.7086 seconds ).
Because I’m interested in both time and frequency domain behavior , I’ve put a lot of effort into designing filters that are as good as possible in both domains simultaneously. IOW that gives you a correct reconstruction from all aspects that are inversely proportional to each other, through a 1/x relationship . This means making a filter that is as short as possible in the time domain (as short ringing as possible) while giving as good a frequency domain reconstruction as possible. I give several filter length options for most filters so that you can choose the optimal balance for your enclosure, from short to very long filters, depending on the requirements of the source content. If you want minimal ringing and optimal time domain response, use the “-short” filters.
There are also completely ring-free interpolators (polynomials) that you can use for both PCM and SDM outputs, but these still have many of the adverse effects of NOS listed above due to incomplete reconstruction.
Coming back to the ringing that is baked into the source content, this is an aspect that can be changed with apodizing filters.Source:Holo Cyan 2 – Page 6 – DAC – Digital-to-Analog Conversion – Audiophile Style (audiophilestyle.com)
Upsampling ratio
“Integer” means that it can only perform even ratio conversions up or down. For example, a 44.1 kHz source cannot be upsampled to 196 kHz by filters with the ” Integer ” property. The correct way to do this would be to upsample it to 176.4 kHz. “Integer up ” means that the filter can only perform conversions to higher rates, but not to a lower rate (eg from 384k to 192k). ” Any ” has no restrictions.
The even ratio conversion is recommended as it generally reduces the computational load.
Compressed music
The problem today is over-compressed music ( loudness war ). This compression of the audio signal leads to a more consistent “audibility” of the music, but also results in a high loss of dynamics. As a result, the upper bands are cut off. With such recordings it is better to convert them to a DSD output with a higher rate. At least DSD256 or even better DSD512, using the EC modulators. Even PCM upsampling to 1.5MHz cannot compete with this, as it sometimes lacks “depth and airiness”.
If it’s a 44.1/48kHz source, using an apodization filter is generally recommended, see above. It’s also good to stick to a shorter filter, such as poly-sinc-short. And possibly minimum phase.
Another approach is to use longer filters, but particularly transient-optimized, such as the poly-sinc Gaussian family:
1x (44.1/48kHz) = poly-sinc-gauss-long
Nx (88.2/96kHz and higher) = poly-sinc-gauss-hires-lp
The developer Jussi Laako is so enthusiastic about this solution that these filters will be pre-defined in the settings in the future.
Table with filter properties
The table lists the most important filters without guarantee. From HQPlayer version 5.20 (September 30, 2023) the new filters will beNEWThe descriptions were taken from the HQPlayer manual and other sources. Links lead to further explanations and measurement results.
| filter | Description | Ratio | Apodi-sizing | genre | focus | Optimized for |
|---|---|---|---|---|---|---|
| poly-sinc-lp | Linear phase polyphase sinc filter. Very high quality linear phase resampling filter, can perform most of the typical conversion ratios. Good phase response but has some degree of pre-echo. | Any | X | Classical | Space | |
| poly-sinc-mp | Minimum phase polyphase sinc filter, otherwise similar to poly-sinc. Modified phase response, but no pre-echo. | Any | X | Jazz, Blues | Transients | |
| poly-sinc-shrt-lp | Otherwise similar to poly-sinc, but shorter pre- and post-echoes at the expense of filter quality (not as sharp roll-off). | Any | X | Jazz, Blues, Electronic | Space, Transients | |
| poly-sinc-shrt-mp | Minimal phase variation of poly-sinc-shrt. Otherwise similar to poly-sinc-mp, but shorter after-echo. Optimal transient reproduction. | Any | X | Pop, Rock | Transients | |
| poly-sinc-long-lp | Similar to Poly-sinc, but longer pre- and post-echoes with improved filter quality (faster roll-off). | Any | X | Classical | Space | |
| poly-sinc-long-ip | Intermediate phase version of Poly-sinc-long, with small pre-echo and longer post-echo with improved filter quality (faster roll-off). | Any | X | Jazz, Blues, Electronic | Space, Transients | |
| poly-sinc-long-mp | Minimal phase variant of poly-sinc-long. Otherwise similar to poly-sinc-mp, but longer after-echo with improved filter quality (faster roll-off). | Any | X | Pop, Rock | Transients | |
| poly-sinc-hb | Linear phase polyphase half-band filter with steep cut-off and high attenuation. By definition, half-band filters pass the original data through unchanged and only add new samples in between. This also means that it cannot correct errors in the source data and thus also reproduces all errors faithfully. This is why it is not suitable for 95% of RedBook content! | Any | ||||
| Poly-sinc-hb-xsNEW | Extremely short linear-phase polyphase half-band filter with slow roll-off and low attenuation. Only suitable for source materials of the highest technical quality. This is almost identical to the one used by Mola-Mola. | Any | Pop, Rock | |||
| poly-sinc-hb-sNEW | Short linear, multiphase half-band filter with shorter roll-off and medium attenuation. Suitable only for source materials of the highest technical quality. | Any | Pop, Rock | |||
| poly-sinc-hb-mNEW | Medium linear polyphase half-band filter with average roll-off and medium attenuation. Suitable only for source materials of the highest technical quality. | Any | ||||
| poly-sinc-hb-lNEW | Long-phase polyphase half-band filter with fast rolloff and high attenuation. Only suitable for source materials of the highest technical quality. | Any | Classical, Jazz, Blues | |||
| poly-sinc-ext | Linear phase Polyphase Sinc filter with sharper cut-off and slightly lower stop band attenuation at approximately the same length as Poly-Sinc. | Integer | X | |||
| poly-sinc-ext2 | Linear phase polyphase sine filter with sharp cut-off and high stopband attenuation for extended frequency response while completely blocked by the Nyquist frequency. For SDM outputs, processing is done in two stages at 16x intermediate rate. One of the aspects that affect the sound of the filter is the shape of the roll-off. | Any | X | Each Genre | timbre | DSD |
| poly-sinc-ext3 | Very steep 8 times longer version of poly-sinc-ext2. | Any | X | Classical | timbre | DSD |
| poly-sinc-mqa/mp3-lp | Linear phase polyphase sinc filter optimized for playback of MQA or MP3 encoded content to remove high frequency noise added by the MQA or MP3 encoding. Also suitable for upsampling PCM sources with 88.2 kHz or higher sample rate, especially for HighRes PCM recordings with 176.4 kHz or higher sample rate. Very short ringing. Early slow roll off. | PCM: Integer up SDM: Any | X | Classical, Jazz, Blues | Transients | MQA/MP3/ HiRes PCM |
| poly-sinc-mqa/mp3-mp | Minimal phase variant of poly-sinc-mqa. | PCM: Integer up SDM: Any | X | Pop, Rock | Transients | MQA/MP3/ HiRes PCM |
| poly-sinc-xtr-lp | Linear phase polyphase sinc filter with extreme cut off and high attenuation. | Any | Classical | timbre | ||
| poly-sinc-xtr-mp | Minimum phase polyphase sinc filter with extreme cut off and high attenuation. | Any | Jazz, Blues | timbre | ||
| poly-sinc-xtr- short-lp | Short linear phase polyphase sinc filter with extreme cut off and high attenuation. | Any | X | Electronic, Jazz, Blues, Pop, Rock | timbre | |
| poly-sinc-xtr- short-mp | Short minimum phase polyphase sinc filter with extreme cut off and high attenuation. | Any | X | Pop, Rock | timbre | |
| poly-sinc-gauss-short | Short Gaussian polyphase sinc filter. Optimal time-frequency response. For SDM outputs, processing occurs in two stages with 16x intermediate rate. | Integer up | X | Electronic, Jazz, Blues, Pop, Rock | Transients | DSD |
| poly-sinc-gauss | Gaussian polyphase sinc filter. Optimal time-frequency response. For SDM outputs, processing occurs in two stages with 16x intermediate rate. | Any | X | Each Genre | Transients, Timbre | DSD |
| poly-sinc-gauss-long | Long Gaussian polyphase sinc filter with extremely high attenuation. Optimal time-frequency response. For SDM outputs, processing is done in two stages at 16x intermediate rate. One of the aspects that influences the sound of the filter is the shape of the roll-off. Flat up to 20 kHz and reaches -300 dB at 22.05 kHz | Any | X | Each Genre | Transients, Timbre, Space | DSD |
| poly-sinc-gauss-xl | Extra long Gaussian polyphase sinc filter with extremely high attenuation. Optimum time-frequency response. For SDM outputs, processing takes place in two stages with 16x intermediate rate. | Any | Classical, Jazz, Blues | Transients, Timbre, Space | DSD | |
| poly-sinc-gauss-xla | Apodizing extra long Gaussian polyphase sinc filter with extremely high attenuation. Optimum time-frequency response. For SDM outputs, processing takes place in two stages with 16x intermediate rate. | Any | X | Classical, Jazz, Blues | Transients, Timbre, Space | DSD |
| poly-sinc-gauss-hires-lp | Linear phase Gaussian filter for HiRes content with extremely high attenuation. Optimum time/frequency response. Also suitable for playback of lossy compression such as MP3 or MQA. | Any | X | Each Genre | Transients, Timbre, Space | |
| poly-sinc-gauss-hires-ip | Medium phase Gaussian filter for HiRes content with extremely high attenuation. Optimum time and frequency response. Also suitable for playback of lossy compression such as MP3 or MQA. | Any | X | Each Genre | Transients, Timbre, Space | |
| poly-sinc-gauss-hires-mp | Gaussian filter with minimum phase for HiRes content with extremely high attenuation. Optimal time/frequency response. Also suitable for playback of lossy compression such as MP3 or MQA. | Any | X | Each Genre | Transients, Timbre, Space | |
poly-sinc-gauss-halfband | Linear phase half-band Gaussian filter. Slight leakage in the Nyquist region, but extremely high attenuation. Only suitable for highest quality source material | Any | Each Genre | Transients, Timbre, Space | ||
| poly-sinc-gauss-halfband-sNEW | Short linear half-band Gaussian filter with lower attenuation and less steep roll-off. Only suitable for source materials of the highest technical quality. | Any | Each Genre | Transients, Timbre, Space | ||
| minringFIR-lp | Minimal ringing FIR. Uses a special algorithm to create a linear phase filter that minimizes the amount of ringing while providing better frequency response and damping than polynomial interpolators. Performance and ringing are between polynomial and poly-sinc-short. | Integer up | Transients | |||
| minringFIR-mp | Minimum phase variant of minringFIR. | Integer up | Transients | |||
| closed-form | Closed form interpolation with high number of taps. | 2x up | ||||
| closed-form- fast | Closed form interpolation with lower CPU load but also lower precision. The output precision is tuned to approximately 24-bit PCM. | 2x up | ||||
| closed-form-M | Closed form interpolation with one million taps. | 2x up | ||||
| closed-form- 16M | Closed form interpolation with 16 million taps. | 2x up | ||||
| sinc-S | Sinc filter with adaptive tap count. The number of taps is 4096 x conversion ratio. Very sharp cut-off and high attenuation. | Integer | X | Each Genre | Space, Timbre | |
| sinc-M | sSnc filter with one million taps. Very sharp cut-off and high attenuation. sinc-M is always a fixed length in the number of taps, regardless of the conversion ratio. sinc-Mx is always a fixed length in time, regardless of the conversion ratio. This means that sinc-M becomes less steep as the ratio increases. While sinc-Mx maintains the same steepness regardless of the conversion ratio. | Integer | X | Classical | Space, Timbre | |
| sinc-Mx | Constant-time version of sinc-M. The filter length is constant in time, with millions of taps at 16x PCM output rates. | Integer | X | Classical, Jazz, Blues | Space, Timbre | |
| sinc-MG | Gaussian constant time filter with one million taps at 16x PCM output rate. Extremely high attenuation. ( 65536 conversion ratio ) | Integer | Classical, Jazz, Blues | Transients, Timbre, Space | ||
| sinc-MGa | Apodizing Gaussian constant-time filter with one million taps at 16x PCM output rate. Extremely high attenuation. ( 65536 conversion ratio ) Similar to poly-sinc-gauss-xla. But previously sinc-MG(a) incorrectly ran “only” 4M taps at a rate of 22.6/24.6 MHz (DSD512), while it should run 32 million taps at that rate, assuming a 44.1/48k source (16 x 32 = 512 ). | Integer | X | Classical, Jazz, Blues | Transients, Timbre, Space | |
| sinc-L | Sinc filter with adaptive tap count. The number of taps is 131070 x conversion ratio. Extremely sharp cut-off and average attenuation. | Integer | Classical | |||
| sinc-Ls | Average attenuation of the sinc filter with adaptive number of taps (4096 x conversion ratio). | Integer | Each Genre | |||
| sinc-Lm | Average attenuation of the sinc filter with adaptive number of taps (16384 x conversion ratio). | Integer | Classical, Jazz, Blues | |||
| sinc-LI | Average attenuation of the sinc filter with adaptive number of taps (65536 x conversion ratio). | Integer | Classical | |||
| sinc-short | Short medium attenuation sinc filter with adaptive number of taps. For SDM outputs, processing consists of two stages with a 16x intermediate rate. | Any | Any | NEW DSD | ||
| sinc-medium | Medium attenuation sinc filter with adaptive number of taps. For SDM outputs, processing consists of two stages with a 16x intermediate rate. | Any | Classical, Jazz, Blues | NEW DSD | ||
| sinc-long | Long medium attenuation sinc filter with adaptive number of taps. For SDM outputs, processing consists of two stages with a 16x intermediate rate. | Any | Classical | NEW DSD | ||
| filter | Description | Ratio | Apodi-sizing | genre | focus | Optimized for |
HQPlayer Filter Selection – Descriptions without guarantee –
Filters with *-2s have two-stage oversampling. The first stage rate conversion is performed by at least a factor of 8 using the selected algorithm. And further converted to the final rate using an algorithm optimized for converting content that has already been processed to at least 8x rate. This lowers the overall CPU load while maintaining conversion quality. Especially useful for highest output rates.



